今では歴史を研究していますが、5年前まではある本がキッカケで数学者になりたかった人です。
どうも、数学大好きっ子のノスクちゃんです
「隣り合う色が同じにならないように地図を塗分けるには最低何色必要でしょうか?」
問題①
例えば、
こんな感じの地図があるとします。
この地図を塗分けるのに必要な色はいくつでしょうか?
答えは2色。

チェス盤のように塗れば二色で十分ですね
問題②
ではこのような地図はどうでしょう?
答えは3色。
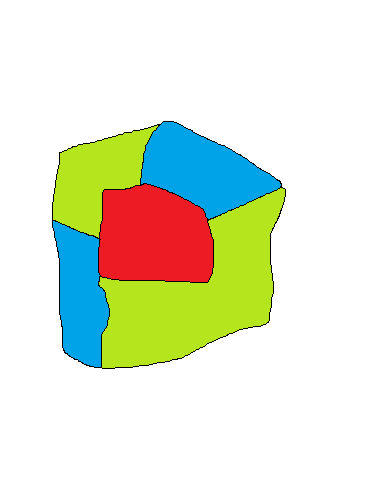
こんな感じ。
問題③
ではこれは?
答えは4色。

こう。
5色以上必要な地図は?
4色まではわかりましたね
ではこのまま地図を複雑にしていった場合、どうなるのでしょうか?
5色、6色と増えるのでしょうか?
実際にやってみましょう。
自分で地図を作るとイカサマできちゃうので、今回はテキトーに、「東京23区」の白地図を国土地理院さんからお借りして、色分けしていきたいと思います。
実際の地図なので不規則な配置となっていますが、果たして何色で塗分けられるのでしょうか??
結果はコチラ!
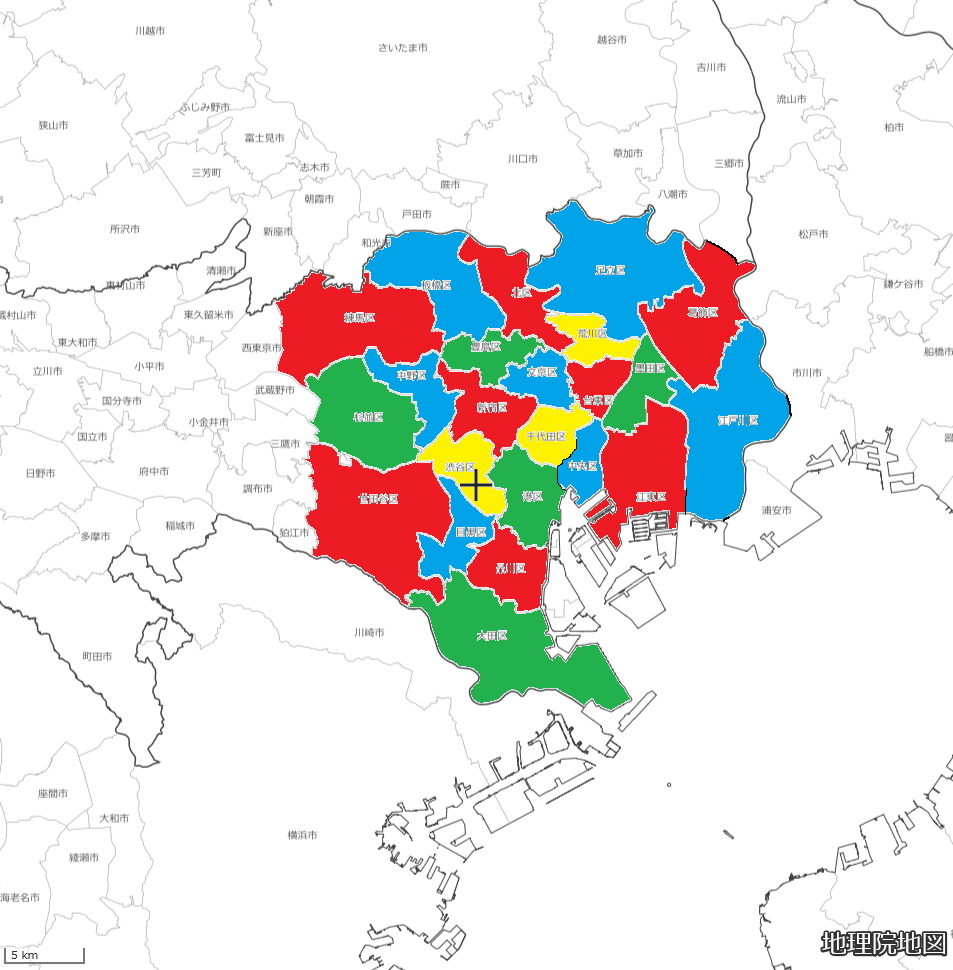
赤、青、緑、黄の四色でぬりわけることができました!
そうなんです、
どんなに複雑な地図でも、4色あれば塗分けられるのです
この問題を四色問題(四色定理)と言います
証明できるの?
さて、証明!、、、、がとても難しいんです。。
三色じゃ無理ということは「三色じゃ塗りきれない地図」を用意できれば証明できますが
五色も必要ないことは証明することが非常に難しいのです。
”ないことの証明”というのは非常に難しくて、「すべてのパターンにおいて当てはまらない」という証明をしていかなければなりません。
しかし、地図のパターンは無数にあるので、それを網羅するのは非常に大変なのです
四色問題の証明
いちおう証明はされています。
されていますが、
結局、コンピューターでゴリゴリ計算して証明したそうです。
手計算で解いた人はまだいないそうです。
証明は相当難しいんですねぇ
以上です~
参考資料↓



